Question

As part of a sweepstakes, Carlos is given one dollar onthe first day. Carlos is told that the number of dollarsgiven each day is double the number given the daybefore. How many dollars will he earn on day 8?

Answer 1

Given that Carlos gets one dollar on the first day, and that the number of dollars given is double the number he gets the previous day.

Thus, from day 1, he gets

`1,\text{ 2, 4, 8, }\ldots`

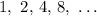
This forms a geometric sequence whose respective terms are evaluated as

`\begin{gathered} T_n=ar^(n-1)-----\text{ equation 1} \\ \text{where } \\ a\Rightarrow first\text{ term of the sequence} \\ r\Rightarrow common\text{ ratio of the sequence, evaluated as the quotient betw}een\text{ } \\ \text{the two consecutive terms} \\ n\text{ }\Rightarrow\text{ the position occupied by the term of the sequence} \\ T_n\Rightarrow value\text{ of the nth term} \end{gathered}`

Thus, from the defined parameters,

`\begin{gathered} a=1 \\ r=(2)/(1)=(4)/(2)=(8)/(4)\text{ =2} \\ n\text{ = 8} \\ T_n\text{ is unknown.} \end{gathered}`

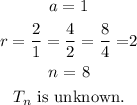
Thus, substitute the above values into equation 1

`\begin{gathered} T_8=1(2)^(8-1) \\ \Rightarrow2^7 \\ T_{8\text{ }}=128 \end{gathered}`

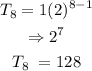
Hence, on day 8, he will receive 128 dollars.

The third option is the correct answer.