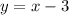Answer
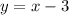
Step-by-step explanation
The equation in slope-intercept form is:

where m is the slope and b is the y-intercept.
Additionally, the slope m can be calculated using the change between two points as it is a line and will be the same in all points:

Considering the two points given, we can assume that point one is (-2, -5) and point two is (-5, -8). Replacing these values we get:
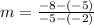
Simplifying:
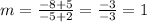
Then, replacing the slope calculated in the equation we get:
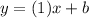
Next, we have to choose one of the given points to replace in the equation and solve for b. For example, choosing (-2,-5):


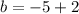
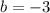
Finally, our equation is: