Question

Can you pls solve this as fast as you can

Answer 1

We are given two similar cones. This means that each corresponding segments of the cones are at the same ratio with each other. We will determine the ratio of the lengths by determine the ratio between the heights of the cones:

`r_l=(h_A)/(h_B)`

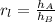
Now, we substitute the heights:

`r_l=(5)/(15)=(1)/(3)`

Therefore, the ratio between the cones is 1/3.

Now, we determine the ratio between the base areas:

`R_A=(A_A)/(A_B)`

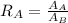
The area of a cone is given by:

`A=\pi r^2`

Now, we substitute the area of each cone:

`R_A=(\pi r_A^2)/(\pi r_B^2)`

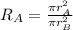
We can cancel out the pi:

`R_A=(r_A^2)/(r_B^2)`

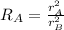
Now, we use a propoerty of exponentials to rewrite the expression:

`R_A=((r_A)/(r_B))^2`

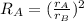
Now, since the radius are length this means that he ratio between them is the same as the length ratio, therefore:

`R_A=((1)/(3))^2=(1)/(9)`

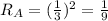
Therefore, we have Ratio the base areas: 1/9.

Now, we determine the ratio between the surface area using the following formula:

`R_(SA)=(S_A)/(S_B)`

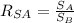
The surface area is given by:

`S=\pi rl`

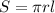
Where:

`l=\text{ slant height}`

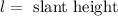
In the given cones, we hace that the slant heights are:

`\begin{gathered} l_A=OM \\ l_B=GE \end{gathered}`

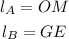
Now, we substitute the values:

`R_(SA)=(\pi r_Al_A)/(\pi r_Bl_B)`

Now, we cancel out the pi:

`R_(SA)=(r_Al_A)/(r_Bl_B)`

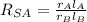
Since the radius and the slant heights are lengths this means that each of their ratios are equal to the length ratio, therefore, we have:

`R_(SA)=((1)/(3))((1)/(3))=(1)/(9)`

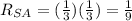
Therefore, we have Ratio of surface area: 1/9

For the volume we will use the following formula:

`R_V=(V_A)/(V_B)`

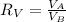
The volume of a cone is given by:

`V=\pi r^2h`

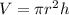
Substituting for each cone we get:

`R_V=(\pi r_A^2h_A)/(\pi r_B^2h_B)`

We can cancel out the pi:

`R_V=(r_A^2h_A)/(r_B^2h_B)`

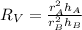
Now, we apply the following property of exponentials:

`(a^x)/(b^x)=((a)/(b))^x`

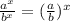
Applying the property we get:

`R_V=((r_A)/(r_B))^2((h_A)/(h_B))`

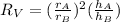
Now, we substitute for the length ratios:

`R_V=((1)/(3))^2((1)/(3))=((1)/(3))^3=(1)/(27)`

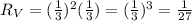
Therefore, Ratio of volumes: 1/27