Given:
Total investment is, T (P) = $21,000.
First type of interest is, r(1) = 4%=0.04.
Second type of interest is, r(2) = 8.5%=0.085.
Annual interest amount is, T (I) = $1,515.00.
The objective is to find the amount invested in each type of interest.
Consider the amount invested in first type as x and the amount invested in second type as y.
Then the equation of total investment can be written as,
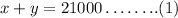
Now, the equation of total interest amount can be written as,
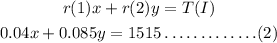
Multiply equation (1) by 0.04.
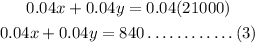
On solving equation (2) and (3),
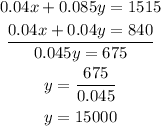
Substitute the value of y in equation (1) to find x.

Hence, the amount invested at 4% is $6000 and the amount invested at 8.5% is $15000.