Question

Consider the following system of equations,4x - 3y = 0- 4x + 3y = 0Step 1 of 2: Determine if the point (3,4) lies on both of the lines in the system of equations by substituting the ordered pair into bothequations

Answer 1

In order to know if the point (3,4) lies on both lines we need to substitute in each equation the value of the coordinate x and if the point lies on the line the y-coordinate must be the same of the given

For the first equation

x=3

`\begin{gathered} 4(3)-3y=0 \\ 12-3y=0 \\ -3y=-12 \\ y=(-12)/(-3) \\ y=4 \end{gathered}`

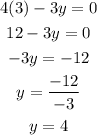
The point calculated is (3,4)

For the second equation

x=3

`\begin{gathered} -4(3)+3y=0 \\ -12+3y=0 \\ 3y=12 \\ y=(12)/(3) \\ y=4 \end{gathered}`

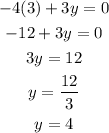
The point calculated is (3,4)

As we can see the points calculated are congruent with the point given therefore the point (3,4) lies on both lines.

ANSWER

YES