What do I even do?? I’ve looked at all my notes & nothing!!

Question

asked Jan 11, 2023 218k views

1 Answer

Zarthross · Answer 1 · 2023-01-16T12:07:08+0000

Given the equation:

Let's solve the equation for x.

To solve for x, the first step is to cross multiply:

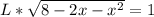
Now, divide both sides by L:

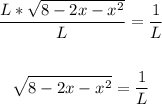
$\begin{gathered} (L*√(8-2x-x^2))/(L)=(1)/(L) \\ \\ √(8-2x-x^2)=(1)/(L) \end{gathered}$

Square both sides:

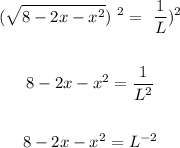
$\begin{gathered} (√(8-2x-x^2))\text{ }^2=\text{ \lparen}(1)/(L))^2 \\ \\ 8-2x-x^2=(1)/(L^2) \\ \\ 8-2x-x^2=L^(-2) \end{gathered}$

Now, subtract L⁻² from both sides and equate to zero:

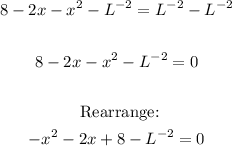
$\begin{gathered} 8-2x-x^2-L^(-2)=L^(-2)-L^(-2) \\ \\ 8-2x-x^2-L^(-2)=0 \\ \\ \text{ Rearrange:} \\ -x^2-2x+8-L^(-2)=0 \end{gathered}$

Solve the equation using the quadratic formula:

$x=(-b\pm√(b^2-4ac))/(2a)$

Where:

a = -1

b = -2

c = (8 - L⁻²)

Thus, we have:

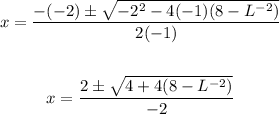
$\begin{gathered} x=\frac{-(-2)\pm\sqrt{-2^2-4(-1)(8-L^(-2))}}{2(-1)} \\ \\ x=\frac{2\pm\sqrt{4+4(8-L^(-2))}}{-2} \end{gathered}$

Therefore, the solution is: