Step 1:
Draw the figure
The diagonals of a rhombus bisect each other,
therefore
FJ = JH
this implies that
JH = 4.
Opposite angles of a rhombus are equal, so
The diagonals of a rhombus bisect the interior angles.
Therefore,
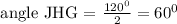
The diagonals of a rhombus are perpendicular
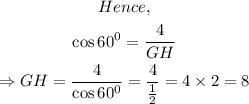
GH = 8 (b)
Also,
Using the Pythagorean rule,
![\begin{gathered} JG^2+4^2=GH^2 \\ \Rightarrow JG^2+16=8^2 \\ \Rightarrow JG=\sqrt[]{64-16}=\sqrt[]{48}=4\sqrt[]{3}=6.928\text{ } \\ \text{right choice is C} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wb03p50gf6z810jud2uqmyh5orpfu856t8.png)
FH = FJ + JH
this implies that
FH = 4 + 4 = 8
FH = 8
right choice B
The diagonals of a rhombus bisect the interior angles.
therefore

Sum of the interior angles of a rhombus is 360degrees.
And opposite interior angles of a polygon are congruent.
Therefore
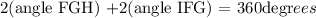

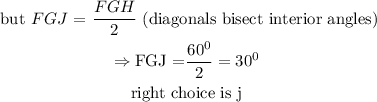
Also,
![\begin{gathered} [tex]\begin{gathered} \text{JGH}=\text{ }(FGH)/(2)=(60)/(2)=30^0 \\ right\text{ choice is j} \end{gathered}]()