Given:
Numbers on a dice = 6
Suppose you roll a pair of the dice and add their totals, let's find the probability that the sum of the numbers is a prime number of a number greater than 5.
Where:
Possible outcomes when two dice are tossed =
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) = 36 outcomes
Possible sum is prime:
(1,1 = 2), (1,2 = 3), (1,4 = 5), (1,6 = 7), (2,1 =3), (2,3 = 5), (2,5 = 7), (3,2 = 5), (3,4 = 7), (4,1= 5), (4,3 = 7), (5,2 = 7), (5,6 = 11), (6,1 = 7), (6,5 = 11) = 15 outcomes
P(sum is greater than 5):
[1][5], [1][6], [2][4], [2][5], [2][6], [3][3], [3][4], [3][5], [3][6],[4][2], [4][3], [4][4], [4][5], [4][6],[5][1], [5][2], [5][3], [5][4], [5][5], [5][6],[6][1], [6][2], [6][3], [6][4], [6][5], [6][6]. ==> 26 outcomes
Here, we can see some numbers are repeating, so we will count them once.
(6, 5), (6, 1), ((5, 6), (5, 2), (4, 3), (3, 4), (2, 5)
= 26 - 7 = 19
Thus, we have:
probability that the sum of the numbers on your dice is a prime number or a number greater than =
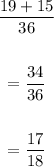
ANSWER:
17/18