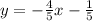Step-by-step explanation
From the statement, we must find an equation:
0. of a line perpendicular to the line 5x - 4y = 6,
,
1. that contains the point (x, y) = (-4, 3).
We write the equation of the given line as:
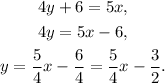
We see that the slope of the given line is m₁ = 5/4.
The slope-intercept equation of the line that we must find is:
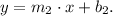
Where:
• m₂ is the slope,
,
• b₂ is the y-intercept.
1) From condition 1, we know that the line must be perpendicular to the given line. So their slopes must satisfy:

Solving for m₂ we get:
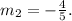
2) Replacing the coordinates of the point from condition 2, and the slope m₂ = -4/5 in the equation of the line, we have:
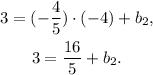
Solving for b₂ we get:
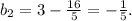
So the slope-intercept equation of the perpendicular line is:
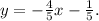
Answer