Question

The Jones family has two dogs whose ages add up to 15 and multiply to 44. Howold is each dog?

Answer 1

Data:

Dog 1: A

Dog 2: B

`\begin{gathered} A+B=15 \\ AB=44 \end{gathered}`

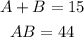
You use substitution method:

1. Solve one variable in one equation:

Solve A in frist equation:

`A=15-B`

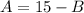
2. Use the solution for the variable in the other equation.

Use A=15-B in the second equation:

`(15-B)B=44`

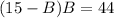
3. Solve the variable.

Solve for B:

`\begin{gathered} 15B-B^2=44 \\ \\ -B^2+15B-44=0 \\ \end{gathered}`

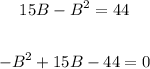
As you get a quadratic function, you need to use a quadratic equation:

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`
`\begin{gathered} B=\frac{-(15)\pm\sqrt[]{(15)^2-4(-1)(-44)}}{2(-1)} \\ \\ B=\frac{-15\pm\sqrt[]{225-176}}{-2} \\ \\ B=\frac{-15\pm\sqrt[]{49}}{-2} \\ \\ B=(-15\pm7)/(-2) \\ \\ B_1=(-15+7)/(-2),B_2=(-15-7)/(-2) \\ \\ B_1=4 \\ B_2=11 \end{gathered}`

4. Use the value of B to find the value of A:

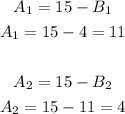
`\begin{gathered} A_1=15-B_1 \\ A_1=15-4=11 \\ \\ A_2=15-B_2 \\ A_2=15-11=4 \end{gathered}`Then, One of the dogs have 11 years and the other dog has 4 years