We can write the equation of the line from the table
The general equation of a line is

where m is the slope and b the y-intercept, the we need to find m and b to replace on the general equation and obtain the function of the line
Slope (m)
We use the formula of the slope
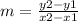
where (x2,y2) is a right point from (x1,y1), I can use any pair of points of the table, on this case I will use (3,228) and (7,532)
where (3,228) is (x1,y1) and (7,532) is (x2,y2)
then replacing
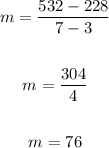
The slope is 76
y-intercept
We repalce the slope on the general equation
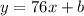
then we replace any point (x,y) for example (11,836)
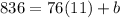
simplify
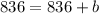
and solve for b
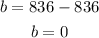
Final equation
replace values of m and b on the general equation to obtaion our linear function
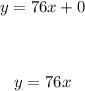
then right option is first, because multiply a number of something by the value of each(76)