Question

You and your friend are two of eight servers working a shift in a restaurant. At the beginning of the shift, the managerrandomly assigns one section to each server. Find the probability that you are assigned Section 1 and your friend is assigned Section 2Express you answer as a fraction in simplest form.

Answer 1

We have 8 sections, numbered from 1 to 8, and 8 servers.

The probability of you being assigned for Section 1 is one into eight (P=1/8) . because we are assuming each of the servers has equal chance of being chosen.

Then, given that you have been assigned to Section 1, there are 7 servers left, including your friend.

Then, there is one into seven chances of your friend being chosen for Section 2 (P=1/7).

We have two events, the first with P=1/8 and the second with P=1/7.

The probability of both of this events happening is the product of their probabilities:

`P=P_1\cdot P_2=(1)/(8)\cdot(1)/(7)=(1)/(56)`

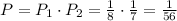
The probability of you being assigned to Section 1 and your friend to Section 2 is P=1/56.