Question

Need help on Q4 thanks all info should be in image

Answer 1

`8.66\text{ }m`

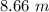
Step-by-step explanation

First, we have to find the frequency of the sound in the air.

To do this, apply the formula for the speed of a wave:

`v=\lambda *f`

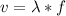
where λ = wavelength

f = frequency

The speed of sound in air is 332 m/s at 0 degrees Celsius.

Hence, using the formula given, the speed of sound in the air of 22 degrees Celsius is:

`\begin{gathered} v=332+0.6*22=332+13.2 \\ v=345.2\text{ }m\/s \end{gathered}`

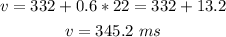
Therefore, the frequency of the sound is:

`\begin{gathered} 345.2=0.785*f \\ f=(345.2)/(0.785) \\ f=439.75\text{ }Hz \end{gathered}`

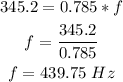
Now, we can apply the formula for the speed of sound in marble to find the wavelength of the wave after it travels into the marble:

`\begin{gathered} v=\lambda *f \\ \lambda=(v)/(f) \end{gathered}`

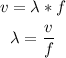
Note: the frequency of the sound in the air and marble are the same

Therefore, the wavelength of the wave after it travels into marble is:

`\begin{gathered} \lambda=(3810)/(439.75) \\ \lambda=8.66\text{ }m \end{gathered}`

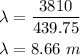
That is the wavelength of the wave after it travels into marble.