Part B: Solving for Isosceles Foods
Isosceles Foods charges $1.10 per burger plus a delivery charge of $52.50
If we were to purchase 300 hamburgers, then
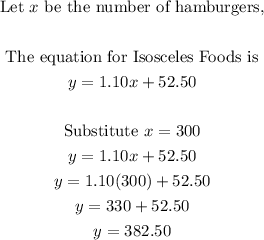
The cost for 300 burgers for Isosceles Foods is $382.50.
Solve for Scalene Wholesale
Scalene Wholesale charges $1.17 per burger plus a delivery charge of $12.25
Purchasing 300 burgers cost

The cost for 300 burgers for Scalene Wholesale is $363.25
Part C: How many hamburgers would have to be purchased so that the cost would be the same for either company.
Equate the two variables such that the variable for number of hamburgers is equal to x, and the cost is the variable y.

Substitute x = 575 for both equations

Therefore, 575 hamburgers would have to be purchased so that the cost is the same for either company ($685).
Part D: Cost
As solved above previously, the cost when for both stored when 575 hamburgers are purchased is $685.
Part E: If 1000 hamburgers are purchased, which company is selected.
Substituting x = 1000, to both equation, we can compare which of the two stores have a cheaper cost.

Comparing the two when purchasing 1000 burgers, Isosceles Foods cost $1152.50, while Scalene Wholesale costs $1182.50.
Therefore, Isosceles would be a better choice since it is cheaper by $30.