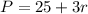Question

George plans to order flowers for his daughter’s graduation. A bouquet of 12 roses will cost $61, while a bouquet of 18 roses will cost $79. What is the equation that represents the linear relationship between price and the number of roses?

Answer 1

Start by finding the slope of the line that passes through both the 12 roses bouquet and the 18 roses bouquet.

point 1: (12,61)

point 2: (18,79)

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ then, \\ m=(79-61)/(18-12) \\ m=(18)/(6) \\ m=3 \end{gathered}`

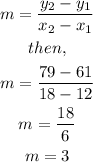
then, using one of the points find the fixed costs

`\begin{gathered} P=m\ast r+b \\ using\text{ \lparen12,61\rparen} \\ 61=3\ast12+b \\ 61-36=b \\ b=25 \end{gathered}`

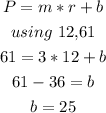
Answer:

The general equation that represents the linear relationship is:

`P=25+3r`