Question

Which of the following pairs of vectors is orthogonal?<2, 9, -2> and <4, -1, 1><3, 1, -5> and <-4,-3 ,-3><4, -1, 3> and <2, 9, 2><-4, 0, 6> and <3, 1, 5>

Answer 1

<3, 1, -5> and <-4,-3 ,-3>

Step-by-step explanation:

Given:

<2, 9, -2> and <4, -1, 1>

<3, 1, -5> and <-4,-3 ,-3>

<4, -1, 3> and <2, 9, 2>

<-4, 0, 6> and <3, 1, 5>

To find:

Which pairs of vectors are orthogonal

Two vectors are said to be orthogonal when their dot product is zero.

So we'll go ahead and determine the dot product of each given pair of vectors as seen below;

For the first pair, we'll have;

`\begin{gathered} <2,9,-2>*<4,-1,1> \\ =2(4)+9(-1)+(-2)(1) \\ =8-9-2 \\ =-3 \end{gathered}`

Since the dot product of this pair isn't zero, these vectors are not orthogonal.

For the second pair, we'll have;

`\begin{gathered} <3,1,-5>*<-4,-3,-3> \\ =3(-4)+1(-3)+(-5)(-3) \\ =-12-3+15 \\ =0 \end{gathered}`

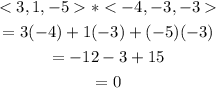
We can see from the above that the dot product of this zero, these vectors are orthogonal.

For the third pair, we'll have;

`\begin{gathered} <4,-1,3>*<2,9,2> \\ =4(2)+(-1)(9)+3(2) \\ =8-9+6 \\ =5 \end{gathered}`

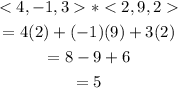
Since the dot product of this pair isn't zero, these vectors are not orthogonal.

For the fourth pair, we'll have;

`\begin{gathered} <-4,0,6>*<3,1,5> \\ =(-4)(3)+0(1)+6(5) \\ =-12+1+30 \\ =19 \end{gathered}`

Since the dot product of this pair isn't zero, these vectors are not orthogonal.