We are asked to determine the equation of a line that passes through the point (-3, -1) and has a slope 2/5. To do that we will use the point-slope form of a line equation:
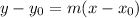
Where:
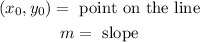
Now, we plug in the values:
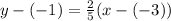
Simplifying we get:
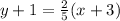
Now, we apply the distributive law:
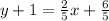
Now, we subtract 1 from both sides:
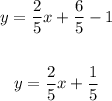
and thus we get the equation of the line.