1) Let's examine the behavior of a rational function and its asymptotes.
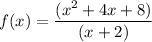
2) Finding the Domain:
D f(x)= x < -2 or x >-2
Let's calculate the Asymptotes:
Vertical Asymptotes
(x-2)
x-2=0
x=-2
Horizontal Asymptotes
y= x+2 because we can find the horizontal asymptotes by considering the coefficients, (x²+4x+8) /(x+2) = (x+2)
y=x+2
3) Let's plot this function along with their asymptotes:
In red and blue we have the asymptotes.
To examine the asymptotic behavior is to talk about limits in another way.
Remember that an asymptote shows us that some of the graphs will not trespass from that point on.
As it is a rational function there are no x-intercepts, the question is what happens when the value as the variable x approaches to 0, note that the graph of y the values that go closer to the asymptote
Let's set a table for that rational function.
Note the values for x= 0 and below how the point gets closer to the asymptote
x | f(x)
0| -4
0.1| -4.42
0.01 | -4.0402
1 | 13
-1.99| -2.01
-1.99| -1.0025
-2 | Undefined
Finally, the table fits to understand a notion of an intuitive notion on limits.
x