We need to find a function of the form:
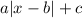
Such that it equals 6 when x=0 and 0 when x=5.
Substitute x=5 and assume that the expression is equal to 0:
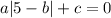
Since the vertex of the function is at the point (5,0), we can assume that c=0.
Therefore:
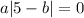
Divide both sides by a:
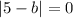
Using that for any number k, |k| = 0 if and only if k=0, then:
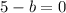
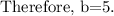
Next, substitute x=0 and assume that the expression is equal to 6 to find a.
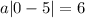
Since |0-5|=5:
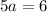
Dividing both sides by 5, we get the value of a:
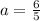
Substitute a=6/5, b=5 and c=0 in the original equation:
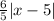
You can check that this expression is equal to 6 when x=0 and it is equal to 0 when x=5.
To find the height at which the second studend should catch the ball, notice that the second student will be placed at x=5+4=9.
Substitute x=9 to find how high will the ball bounce for the second student to catch it:
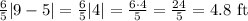
To summarize:
