Hello there. To solve this question, we'll have to remember some properties about slope of a line.
In order to find the constant rate of change of the function represented in the table below, we first have to remember why does it means that the function is a line.
Knowing the instantaneous rate of change of a function f(x) is given by its derivative, i. e.
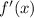
And say this rate of change is constant, that is

Integrating both sides of the equation with respect to x, we have that:
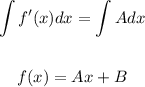
Where A and B are constants, therefore f(x) is the equation of a line.
In fact, this constant rate of change is the slope of the line, so we simply need to find it.
Given two points (x0, y0) and (x1, y1) from the equation of a line, we can find its slope m by using the following formula:
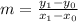
Taking two points from the table, say (-1, 7) and (3, -9), we plug in the formula to find:
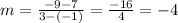
Therefore the slope of this line, and constant rate of change of this function is equal to -4 and it is the answer contained in the option H.