Question

A tortoise can run with a speed of 0.15 m/s, and a hare can run 20 times as fast. In a race, they both start at the same time, but the hare stops to rest for 2.0 minutes. The tortoise wins by a shell (40 cm).(a) How long does the race take? s(b) What is the length of the race? m

Answer 1

From the problem we know that both animals are running at constant speed and on a straight line, this means that the motion of both of them is a rectilinear motion and that their positions can be described as:

`x=x_0+vt`

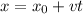
where x is the position at any given time, x0 is their initial position, v is the velocity and t is the time.

Now, let x be the length the hare ran; we know that its velocity is 20 times the velocity of the tortoise which means that it ran at 3 m/s; finally, we also know that it ran 2 minutes less than the tortoise, if we let t be the time the tortoise ran then the time the hare ran is t-120 (in seconds). Hence the position of the hare at any given time is:

`\begin{gathered} x=3(t-120) \\ x=3t-360 \end{gathered}`

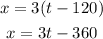
For the tortoise we know that it ran 40 cm more than the hare (to the finish line) and that its velocity was 0.15 m/s, then for the tortoise we have:

`\begin{gathered} x+0.4=0.15t \\ x=0.15t-0.4 \end{gathered}`

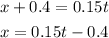
Hence we have the system of equations:

`\begin{gathered} x=3t-360 \\ x=0.15t-0.4 \end{gathered}`

Equating the x variable we have that:

`\begin{gathered} 3t-360=0.15t-0.4 \\ 3t-0.15t=360-0.4 \\ 2.85t=359.6 \\ t=(359.6)/(2.85) \\ t=126.18 \end{gathered}`

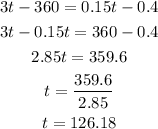
Now that we have the value of t we can find the value of x:

`\begin{gathered} x=3(126.18)-360 \\ x=18.53 \end{gathered}`

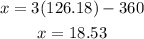
Therefore, the race took 126.18 seconds and its length was 18.53 m