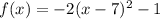Question

F(x) = -2x²+28x -99 in vertex form

Answer 1

The expression we have is:

`f\mleft(x\mright)=-2x^2+28x-99`

Since this is a quadratic equation, is the equation of a parabola in standard form:

`f(x)=ax^2+bx+c`

In this case, comparing the general form and the equation we have:

`\begin{gathered} a=-2 \\ b=28 \\ c=-99 \end{gathered}`

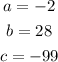
We will define the vertex of the parabola as (h,k). And the general vertex form is:

`f(x)=a(x-h)^2+k`

Where h is defined as follows:

`h=(-b)/(2a)`

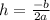
We already know b and a, so we substitute them to find h:

`h=(-28)/(2(-2))=(-28)/(-4)=7`
`h=7`

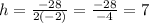
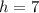
Now we only need to find k, which is defined as the value of the function when x=h:

`k=f(h)`

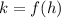
So we find f(h) by substituting h=7 into the original expression:

`\begin{gathered} f(x)=-2x^2+28x-99 \\ k=f(h)=-2(7)^2+28(7)-99 \end{gathered}`

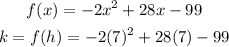
Solving the operations to find k:

`\begin{gathered} k=-2(49)+196-99 \\ k=-98+196-99 \\ k=-1 \end{gathered}`

Now that we have h and k, we go back to the general vertex form:

`f(x)=a(x-h)^2+k`

And substitute a=-2, h=7 and k=-1:

`f(x)=-2(x-7)^2-1`

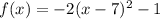
Answer:

`f(x)=-2(x-7)^2-1`