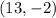We have a line with two points, a conchoidal point, an endpoint and the midpoint.
Point A will be (-5,8) and the unknown endpoint which we will call B will be (x,y).
The midpoint of AB is (4,3), to find point B, We need to use our generalized midpoint formula:
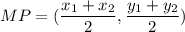
Now, we can replace the known values
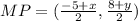
Solve each separately:
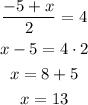
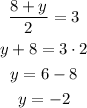
In conclusion, the ordered pair for the other endpoint of the line segment is: