Question

Can someone give me a step by step explanation on how to solve this problem? thank u!

Answer 1

Given that

`f(x)=(1)/(4)x-1\text{ and g(x)=}(1)/(2)x-2`

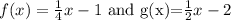
Compare with the slope-intercept form

`y=mx+c`

where m is the slope of the line and c is the y-intercept.

Here:

Slope of f(x) = 1/4

Slope of g(x) = 1/2

y-intercept of f(x) = -1

y-intercept of g(x) =-2

Since 1/2 > 1/4, that is, slope of g(x) > slope of f(x), g(x) is steeper than f(x).

Now, -2 < -1. So, y-intercept of g(x) is less than the y-intercept of f(x). So, g(x) is steeper and has a lower y-intercept.

Hence the third option is correct.