Given the model:
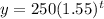
The model above represents the value of a pair of OFF-white Jordan, where t is the number of years since the shoe was released.
Let's answer the following questions.
• a) Let's determine if the model represents an exponential growth or decay.
Apply the exponential function:
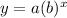
When b is greater than 1, we can say the function reppresents exponential grwoth.
When b is less than 1, the funcrion represents exponential decay.
Here, b = 1.55 is greater than 1.
Since b is greater than 1, the given model represents an exponential growth.
• b) Take the exponential growth function:
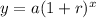
Where:
r = percentage increase.
Since the model is an exponential growth, we are to find the annual percent increase.
To find the annula percentage increase, we have:
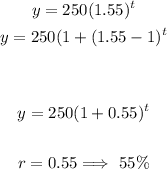
Therefore, the annual percent increase (r) is = 55%
• c) To find when the resale value of the shoe will be over 2000, substitute 2000 for y and solve for t.
Thus, we have:
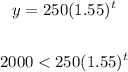
Let's solve for t.
Divide both sides by 250
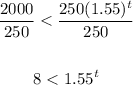
Take the natural logarithm of both sides:
![\begin{gathered} \ln 8Divide both sides by ln1.55:[tex]\begin{gathered} (\ln 8)/(\ln 1.55)<(t\ln1.55)/(\ln1.55) \\ \\ (\ln 8)/(\ln 1.55)(\ln8)/(\ln1.55)=(2.079)/(0.438) \\ \\ t>4.7\approx5 \\ \\ \end{gathered}]()
Therefore, the shoe's resale value will be over $2000 after 5 years
ANSWER:
• a) Exponential growth
,
• b) 55%
,
• c) 5 years