We have that the vertex is (2,0) and the co vertex is (0,1). Since the center is at the origin, we have the following:
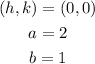
then, the standard form of the equation of the ellipse is:
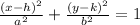
then, in this case,we have the following:
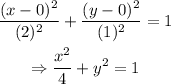
therefore, the equation of the ellipse is x^2 /4 +y^2 = 1