Dimensions of freezer A is 1 foot by 1 foot by 5 foot.
Therefore, the volume of the freezer A is
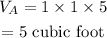
The prize of freezer A per cubic foot is
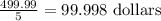
Dimensions of the freezer B is 1.5 feet by 1.5 feet by 4 feet.
Therefore, the volume of the freezer B is
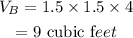
The prize of the freezer B er cubic foot is
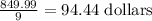
Since, the price of freezer B per cubic foot is lower than that of the freezer A, therefore, freezer B is a better buy.