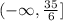Question

Solve the inequality and graph the solution set. Write the solution set in (a) set-builder notation and (b) interval notation. Expressnumbers as integers or simplified fractions.2/5(3z-5)≤5

Answer 1

Step-by-step explanation

Solving the inequality

`\begin{gathered} (2)/(5)(3z-5)\leq5 \\ \text{ Multiply by 5 from both sides} \\ 5\cdot(2)/(5)(3z-5)\leq5\cdot5 \\ 2(3z-5)\leq25 \\ \text{ Apply the distributive property on the left side} \\ 2\cdot3z-2\cdot5\leq25 \\ 6z-10\leq25 \\ \text{ Add 10 from both sides} \\ 6z-10+10\leq25+10 \\ 6z\leq35 \\ \text{ Divide by 6 from both sides} \\ (6z)/(6)\leq(35)/(6) \\ z\leq(35)/(6) \end{gathered}`

Graphing the solution set

Step 1: We draw a number line of a suitable length.

Step 2: Since 35/6 is an improper fraction, we can convert it to a mixed number.

`(35)/(6)=(30+5)/(6)=(5\cdot6+5)/(6)=5(5)/(6)`

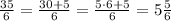
Step 3: Since the proper fraction is 5/6 and the whole number is 5, we divide the unit between 5 and 6 into six parts and place the number on the fifth part.

Step 4: Since the symbol of the inequality is ≤, we fill the dot and draw a line from the left to the marked point.

Answer

a) set-builder notation

`\lbrace z|z\leq(35)/(6)\rbrace`

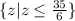
b) interval notation

`(-\infty,(35)/(6)\rbrack`