Question

What are the coordinates of the vertices of the conic section shown below? (x+2) - (-3) = x ² y 1 16 O A (-2-7) and (-2,1) O B. (-6,3) and (2,3) O C (-2,-1) and (-2,7) OD. (2.3) and (63)

Answer 1

Notice that, since the first term is (x+2)^2, we dealing with a hyperbola that is parallel to the x-axis and centered in (-2,3).

The general form of a hyperbola centered in (c,d), and parallel to the x-axis is:

`((x-c)^2)/(a^2)-((y-d)^2)/(b^2)=1`

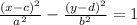
Where a is the horizontal distance between the center of the hyperbola and the vertices.

Then, in our case:

`\begin{gathered} (-2,3)\to\text{center} \\ a=\pm4 \\ \Rightarrow(-2-4,3)=(-6,3),(-2+4,3)=(2,3)_{} \\ \text{are the vertices} \end{gathered}`

The answer is (-6,3) and (2,3), the second option