SOLUTION
A conic with center, vertex and focus is an Elispse
Write out the givencoordinates
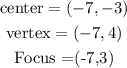
Since the x-coordinate of the given vertices and foci are the same, the equation becomes
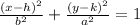
Where

Then
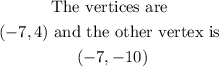
Hence
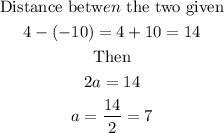
Then
From the given coordinates of the focus (h,k±c) and center (h,k)
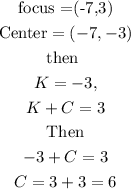
hence

Using

Recall the standard equation as
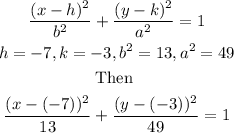
Therefore
The standard equation becomes
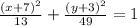
Therefore the standard equation is of the conic is (x+7)²/13 + (y+3)²/49=1