Question

Use the following information for problems 1-3.Applicants to Price Acting School are required to take the Acting Readiness Exam (ARE). Scores on this exam are roughly normally distributed, with a mean score of 63 and a standard deviation of 7. For the upcoming school year, there were 1,000 applicants.How many applicants likely scored higher than 70 on the ARE?95% of applicants could be expected to score within what range?Any applicants who score higher than 84 on the ARE are awarded a certificate of achievement. For the upcoming school year, how many such certificates will be needed?Use the following information for problems 4-6.The mean weight of a domestic house cat is 8.9 pounds, with a standard deviation of 1.1 pounds.The distribution of domestic house cat weights can reasonably be approximated by a normal distribution.What percentage of domestic house cats weigh less than 7.8 pounds?What percentage of domestic house cats weigh more than 11.1 pounds?A domestic house cat weighing 9 pounds is in what percentile?Use the following information for problems 7-9.An article in a health magazine suggested getting a dog in order to increase time spent walking (for exercise). A researcher for the article found that the distribution of time spent walking by dog-owners was approximately normally distributed with a mean of 38 minutes per day. She also found that 84% of dog-owners spend less than 45 minutes walking per day.Find the standard deviation (in minutes) for daily walking time among dog-owners.Construct a normal distribution curve that displays all relevant data for this scenario.How long would a dog-owner need to walk in a day to be ranked in the 99th percentile?Using any research tools at your disposal, find 3 real-world examples of variables that are, in fact, normally distributed.

Answer 1

Exercise 1

We have the following data for the applicants:

• their scores are normally distributed,

,

• the mean score is μ = 63,

,

• the standard deviation is σ = 7,

,

• the number of applicants is n = 1000.

1) How many applicants likely scored higher than 70 on the ARE?

The number of students that will score higher than 70 is given by:

`N=n\cdot P(x\ge70),`

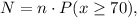
where:

• n is the total number of students,

,

• P(x ≥ 70) is the probability that a student gets a score x ≥ 70.

To compute the probability needed, we compute the corresponding z-score for this case:

`z=(x-\mu)/(\sigma)=(70-63)/(7)=1._{}`

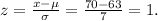
Using the properties of the normal distribution, and table for the z-scores, we have that:

`P(x\ge70)=P(z\ge1)=0.1587.`

Replacing in the formula above, the number of students that will score higher than 70 is:

`N=n\cdot P(x\ge70)=1000\cdot0.1587=158.7\cong159.`

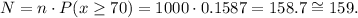
2) 95% of applicants could be expected to score within what range?

To answer this question, we use the Empirical Rule for normal distributions: "The Empirical Rule states that 99.7% of data observed following a normal distribution lies within 3 standard deviations of the mean. Under this rule, 68% of the data falls within one standard deviation, 95% within two standard deviations, and 99.7% within three standard deviations from the mean".

In this case, the rule states that we expect to have 95% of applicants with scores within the following range of scores:

`(\mu-2\sigma,\mu+2\sigma)=(63-2\cdot7,63+2\cdot7)=(49,77)\text{.}`

3) Any applicants who score higher than 84 on the ARE are awarded a certificate of achievement. For the upcoming school year, how many such certificates will be needed?

The number of students that will score higher than 84 is given by:

`N=n\cdot P(x\ge84)\text{.}`

We compute the probability as before. The z-score for this case is:

`z=(x-\mu)/(\sigma)=(84-63)/(7)=3.`

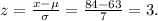
Using a table for z-scores, we find that the probability is:

`P(x\ge84)=P(z\ge3)=0.0013.`

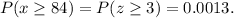
Replacing in the formula above, we find that the number of certificates needed for students with scores higher than 84 is:

`N=n\cdot P(x\ge84)=1000\cdot0.0013=1.3\cong1.`

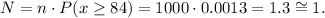
Answers

0. The number of applicants likely to score higher than 70 on the exam is 159.

,

1. It is expected to have 95% of applicants with scores in the range: 49 ≤ x ≤ 77.

,

2. It will be needed 1 certificate for the upcoming school year.