Question

15) Megan is standing on a point that is 40°16' N.

Sarah is at 39°20' N and on the same line of
longitude as Megan. In what direction must
Megan travel to join Sarah?
A) north
B) south
C) east
D) west

Answer 1

Given that Megan is standing on a point that is 40°16' N, coverting Megan's bearing to degree gives

`\begin{gathered} 40^(\circ)16^(\prime)N=40^(\circ)\text{ + (}\frac{\text{16}}{60})^(\circ) \\ =\text{ 40 + 0.}267 \\ =40.267^(\circ)\text{ N} \\ Note\colon1^(\circ)\Rightarrow60^(\prime) \end{gathered}`

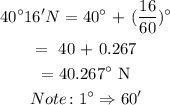
On the same line of longitude as Megan, Sarah is at 39°20' N. Similarly, converting her bearing to degree gives

`\begin{gathered} 39^(\circ)20^(\prime)N=39^(\circ)\text{ + (}(20)/(60))^(\circ) \\ =39+0.333 \\ =39.333^(\circ)\text{ N} \end{gathered}`

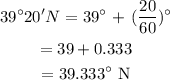
Thus, we have the bearings of Megan and Sarah to be as shown below:

In the above diagram, Megan is at the East of Sarah.

Hence, for Megan to join Sarah, she (Megan) must travel in the West direction.

The correct option is D.