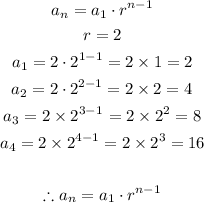Question

Write the recursive and explicit functions the following geometric sequence.2, 4, 8, 16.

Answer 1

We were given the following numbers:

`2,4,8,16`

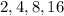
We are to write the recursive and explicit functions for this geometric function.

A recursive function is one that requires that the previous term be known to obtain the successive term in the sequence

An explicit function is one that defines the value of a term based on its current position in the sequence

This is shown below:

`\begin{gathered} a_1=2 \\ a_2=4 \\ a_3=8 \\ a_4=16 \\ r=(a_2)/(a_1)\equiv(a_3)/(a_2)\equiv(a_4)/(a_3)\equiv(4)/(2)\equiv(8)/(4)\equiv(16)/(8)=2 \\ r=2 \end{gathered}`

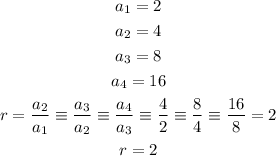
For the Recursive function, we have:

`\begin{gathered} a_n=r\cdot a_(n-1) \\ a_1=2 \\ r=2 \\ \Rightarrow a_n=2\cdot a_(n-1) \\ \text{Let's check if this is true:} \\ when\colon n=2 \\ a_2=2\cdot a_(2-1)\Rightarrow a_2=2\cdot a_1\Rightarrow a_2=2\cdot2=4 \\ when\colon n=3 \\ a_3=2\cdot a_(3-1)\Rightarrow a_3=2\cdot a_2\Rightarrow a_3=2\cdot4=8 \\ \\ \therefore a_n=2\cdot a_(n-1) \end{gathered}`

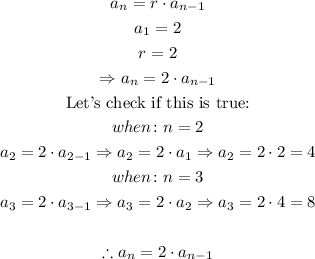
For the Explicit function, we have:

`\begin{gathered} a_n=a_1\cdot r^(n-1) \\ r=2 \\ a_1=2\cdot2^(1-1)=2*1=2 \\ a_2=2\cdot2^(2-1)=2*2=4^{} \\ a_3=2*2^(3-1)^{}=2*2^2=8 \\ a_4=2*2^(4-1)=2*2^3=16 \\ \\ \therefore a_n=a_1\cdot r^(n-1) \end{gathered}`