Question

You know that students at UWS are 55% likely to own a car. You poll 500 UWS students and ask if they own car. Find the probability the number of students who say yes, they do own a car, is between 270 and 290.I want answer with step by step.

Answer 1

Given:

P = 55% = 0.55

n = 500

Let's find the probability the number of students who say yes, they do won a car is between 270 and 290.

Now, let's first find the mean:

`\mu=np=500*0.55=275`

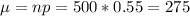
Let's find the standard deviation:

`\begin{gathered} \sigma=√(npq) \\ \\ =√(500*0.55*1-0.55) \\ \\ =\sqrt[]{500*0.55*0.45} \\ \\ =11.12 \end{gathered}`

Now, to find the probability, apply the formula:

`z=(x-\mu)/(\sigma)`

`P(270\leq x\leq290)=(270-275)/(11.12)\leq x\leq(290-275)/(11.12)`

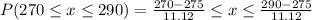
Solving further, we have:

`=−0.44964\leq x\leq1.34892`

Where:

P(270 < x < 290) = P(290) - P(270)

Using the standard normal table, we have:

NORMSDIST(-0.44964) = 0.32649

NORMSDIST(1.34892) = 0.91132

Hence, we have:

P(270 ≤ x ≤ 290 = P(290) - P(2870) = 0.91132 - 0.32649 = 0.58483

Therefore, the probability the number of students who say they own a car is between 270 and 290 is 0.585

ANSWER:

0.585