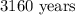Let C be the total amount of C-14, after a time t from the origin of the piece of wood. If the initial amount of C-14 is C_0, and the half-life of C-14is τ, then, the formula that relates these variables, is:
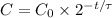
Isolate t from the equation:
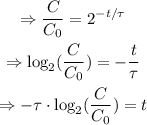
Therefore:
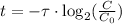
Since the ratio r between the initial amount of C-14 and C-12 is given, we can find the initial amount of C-14:
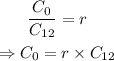
Substitute r=1.20*10^-12 and C_12=1.202*10^-2 mol to find the initial amount of C-14:
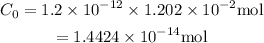
Substitute τ=5730y, C_0=1.4414*10^-14 mol, and C=9.843*10^-15 mol into the formula to find t, which is the age of the wood from the sample:
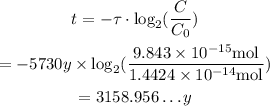
Therefore, to the nearest ten, the age of the sample of wood in the tomb, is: