Given the figure of a square pyramid
As shown, the base is a square with a side length = 6
And the slant height = 5
We will find the following:
a) The height of the pyramid
We will use the Pythagorean theorem to find the height of the pyramid
As shown in the following figure:
The height = h
The value of x = 6/2 = 3
So, there is a right angle triangle with legs of 3 and (h) and the
hypotenuse = 5
So, we will find (h) as follows:
![\begin{gathered} h^2+3^2=5^2 \\ h^2=5^2-3^2=25-9=16 \\ h=\sqrt[]{16}=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k55adfdh5qw76uft6w5mejz2yajaesgg4f.png)
So, the answer will be option C. 4
============================================================
b) The volume of the pyramid
The volume of the pyramid will be calculated using the following formula:
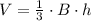
Where B is the area of the base, (h) is the height of the pyramid
So, the volume will be as follows:
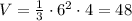
So, the answer will be option A. 48
================================================================
c) The surface area of the pyramid
The surface area = the area of the base + area of the triangular sides
The triangular sides have the same equal base = 6
And the same height = 5
So, the surface area =
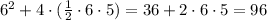
So, the answer will be option C. 96
===================================================================
d) The horizontal cross-section (that is not the base) is a dilation of the base using the apex as a center of dilation
So, the dilation factor will be less than 1 as the length decrease as we goes to the apex
so, the answer will be option B. 1/2