assignmentYou have to answer 300 questions.
You start at 5:00 and by 6:30 you have answered 55 questions. → the time that passed by is one hour and 30 minutes. To make the calculations easier I will express the time in minutes.
1 hour has 60 minutes, so 1 hour and 30 minutes has a total of 60+30=90 minutes
So, in 90minutes, 55 questions were answered.
Considering that the timer per question answered follows the same rate, you can use cross multiplication to determine how much time it will take to answer the 300 questions:
55 questions _____ 90 minutes
300 questions ____ x minutes
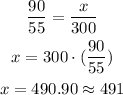
It will take you 491 minutes to answer all questions.
Now you have to express the minutes as hours, for this, divide 491 by the number of minutes in 1 hour (i.e. 60 minutes)
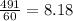
This indicates that it will take a little more than 8 hours to finish the questions.
If you multiply the decimals "0.18" by 60 you'll get the number of minutes
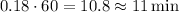
So it will take 8 hours and 11 minutes to solve the 300 questions.
If you start answering at 5:00 without any break, add the time calculated to determine the time you will finish the assignment:
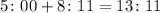
You will finish the assignment at 13:11
Given the linear function that represents the remaining questions, Q, after h hours of work
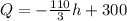
You have to determine how much time it will take to finish the assignment, that is, the value of h for Q=0 (no questions remaining), you have to equal the equation to zero
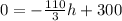
Now you have to calculate the value of h, first, subtract 300 from both sides of the equation
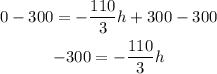
Next, you have to divide the equation by -110/3 to reach the value of h, or since it is a fraction, you can multiply both sides of the equation by the reciprocal (inverse) fraction -3/110
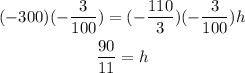
The time it takes to solve all 300 questions is h=90/11 hours or expressed as a decimal value 8.18 hours