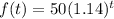Question

The number of ants in a colony was 50 in 1996 and has increased by 14% each year. Which exponential growth model shows the number of aunts in the colony in terms of t, the number of years since 1996?

Answer 1

Given that;

The number of ants in a colony was 50 in 1996 and has increased by 14% each year.

The formula for exponential growth is

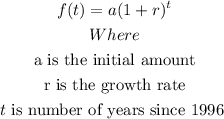
`\begin{gathered} f(t)=a(1+r)^t \\ Where \\ \text{a is the initial amount} \\ \text{r is the growth rate} \\ t\text{ is number of years since 1996 } \end{gathered}`

Where

`\begin{gathered} a=50 \\ r=(14)/(100)=0.14 \end{gathered}`

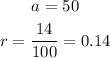
Substitute the values of the variables, a and r into the exponential growth formula above

`\begin{gathered} f(t)=50(1+0.14)^t=50(1.14)^t \\ f(t)=50(1.14)^t \end{gathered}`

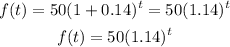
Hence, the equation that models the exponential growth is

`f(t)=50(1.14)^(t)`