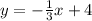Answer:
From the graph, we can see that line AB passes through the points (-3, 5) and (3,3)
We know that the slope-intercept form of the equation of the lines goes by:

Where:
m = slope
b = y-intercept
To get the slope, we are going to use the following formula:

Again, with the points (-3, 5) and (3, 3), we will substitute the corresponding values to the formula
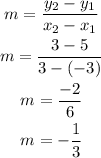
Now, we got a slope of -1/3. Next, we need to find the y-intercept (b). We are going to solve it by using the formula y = mx + b, while substituting the point (-3, 5) and the slope -1/3.
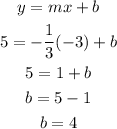
We now have the value of our y-intercept. Since we now have both slope (m) and y-intercept (b), we will substitute both values to the slope-intercept form of the equation of the line to get the final answer.
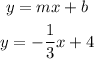
Therefore, the final answer is: