The given sequence is
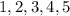
Explicit Rule:
The standard explicit formula for an arithmetic sequence is given by

Where aₙ is the nth term, a₁ is the first term and d is the common difference
The common difference is basically the difference between any two consecutive terms
d = 5 - 4 = 1
d = 4 - 3 = 1
d = 3 - 2 = 1
So the common difference = 1
As you can see, the first term = 1
So the explicit formula for the given arithmetic sequence becomes
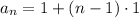
You can find any term by using the above formula.
For example:
if you want to find the 10th term then substitute n = 10 in the above formula.
Recursive Rule:
The standard recursive formula for an arithmetic sequence is given by
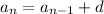
Where aₙ is the nth term, a(n-1) is the previous term and d is the common difference
We already know common difference = 1
So the recursive formula for the given arithmetic sequence becomes
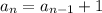
This simply means that if you know the previous term then you add 1 to get the next term.