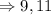Question

Find two consecutive positive odd integers have a product of 99. Find the integers

Answer 1

Let the first odd number be

`=x`

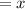
Let the second odd number be

`x+2`

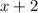
The product of the consecutive odd numbers is 99 and this will be represented below as

`x(x+2)=99`

By expanding the bracket, we will have

`\begin{gathered} x(x+2)=99 \\ x^2+2x=99 \\ x^2+2x-99=0 \end{gathered}`

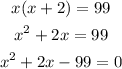
By using the quadratic formula, we will have that

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ a=1,b=2,c=-99 \end{gathered}`

By substituting the values in the formula, we will have

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ x=(-2\pm√((-2)^2-4*1*(-99)))/(2*1) \\ x=(-2\pm√(4+396))/(2) \\ x=(-2\pm√(400))/(2) \\ x=(-2\pm20)/(2) \\ x=(-2+20)/(2),x=(-2-20)/(2) \\ x=(18)/(2),x=-(22)/(2) \\ x=9,x=-11 \end{gathered}`

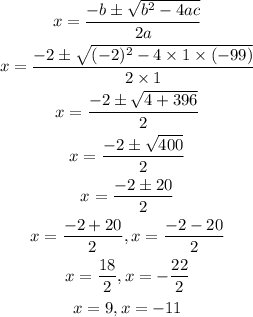
Substitute x=9 in the expression below

`\begin{gathered} x+2 \\ =9+2 \\ =11 \end{gathered}`

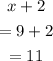
Hence,

The consecutive positive odd integers are

`\Rightarrow9,11`