The given line is
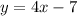
Since the equation is in slope-intercept form, we can deduct that its slope is m = 4.
It is important to know that a perpendicular line would have an opposite and reciprocal slope, which is -1/4, that's the slope of the new perpendicular line.
Then, we use the point-slope formula

Where,
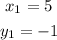

Hence, the answer is y = -1/4x + 1/4.
On the other hand, the equation y = 3 refers to a horizontal line that passes through (0,3).
A perpendicular line that passes through (4, -2) would be x = 4 because it would represent a vertical line that passes through that point.
Hence, the answer is x = 4.