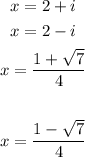Part A
Divide the given polynomial by (m+1/2)
so
2m^3 - 5m^2 -13m -5 : (m+0.5)
2m^2-6m-10
-2m^3-m^2
-----------------------------
-6m^2-13m-5
6m^2+3m
---------------------
-10m-5
10m+5
-----------
0
therefore
2m^3 - 5m^2 -13m -5=(x+0.5)(2m^2-6m-10)
Now, solve the quadratic equation
2m^2-6m-10=0
a=2
b=-6
c=-10
substitute in the formula
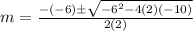
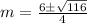
Therefore
The roots of the given equation are
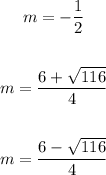
Part B
we have
2x^4 -9x^3 + 13x^2 -x -5=0
one root is (2+i)
by the conjugate theorem
another root must be equal to (2-i)
The factors are
[x-(2+i)] and [x-(2-i)]
Multiply both factors
[x-(2+i)]*[x-(2-i)]=x^2-x(2-i)-x(2+i)+(2+i)(2-i)=x^2-2x+xi-2x-xi+4-i^2
simplify
x^2-4x+4-i^2
i^2=-1
substitute
x^2-4x+4-(-1)
x^2-4x+5
Now, divide
2x^4 -9x^3 + 13x^2 -x -5 by (x^2-4x+5)
2x^4 -9x^3 + 13x^2 -x -5 : (x^2-4x+5)
2x^2-x-1
-2x^4+8x^3-10x^2
----------------------------------
-x^3+3x^2-x-5
x^3-4x^2+5x
---------------------
-x^2+4x-5
x^2-4x+5
---------------
0
Now solve the quadratic equation 2x^2-x+1 using the formula
2x^2-x+1=0
a=2
b=-1
c=1
substitute
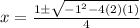
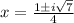
therefore
The roots are