Question

Solve the following series. Remember to use your formulas and indicate your final answer. Find the sum of the first 13 terms of: 1, 2, 4, 8, 16, ...

Answer 1

Sum of the first 13 terms = 8191

Step-by-step explanation

The sum of terms in a geometric term is given as

`S_n=(a\lbrack r^n-1\rbrack)/(r-1)`

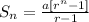
where

a = first term = 1

r = common ratio = ratio of consecutive terms = (Second term)/(First term) = (2/1) = 2

n = number of terms = 13

`\begin{gathered} S_n=(a\lbrack r^n-1\rbrack)/(r-1) \\ S_(13)=(1\lbrack2^(13)-1\rbrack)/(2-1)=(8192-1)/(1)=8191 \end{gathered}`

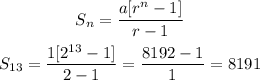
Hope this Helps!!!