Question

Between 1989 and 1998, the population of Smalltown, USA (in thousands) can be modeled by f(x)=0.81x²- 6.48x+17, where x=0 represents 1989. Based on this model, in what year did the population of Smalltown reach its minimum?

Answer 1

The population of small town is modeled by the quadratic function

`f\mleft(x\mright)=0.81x^(2)-6.48x+17`

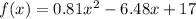
This function forms a parabola that opens upwards, which means that its minimum point corresponds to its vertex.

To determine the direction of the parabola without graphing it you have to look at the sign of the coefficient of the quadratic term, named "a"

If "a" is positive, the parabola opens up

If "a" is negative, the parabola opens down

Now to determine the x-coordinate of the vertex of a quadratic function expressed in standard form you have to use the following formula:

`x_v=-(b)/(2a)`

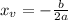
For the given function

a= 0.81

b=-6.48

`\begin{gathered} x_v=-(-6.48)/(2\cdot0.81) \\ x_v=(6.48)/(1.62) \\ x_v=4 \end{gathered}`

Next is to calculate the y-coordinate of the vertex, to do so, replace the x-coordinate in the function

`\begin{gathered} f(x)=0.81x^2-6.48x+17 \\ f(4)=0.81(4^2)-6.48\cdot4+17 \\ f(4)=12.96-25.92+17 \\ f(4)=4.04 \end{gathered}`

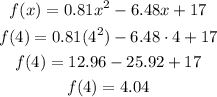
The coordinates of the vertex are:

`(4,4.04)`

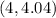
If x=0 represents the year 1989

Then x=4 represents 4 more years: 1989+4=1993

This means that the population of Smalltown reached its minimum in year 1993