Question

When conducting objects (such as metals) are connected for a brief time, charge can be made to flow quite easily from one to the other, even if the objects are in contact for an extremely brief amount of time. To that end, consider two identical metallic ball bearings (i.e., two very tiny metallic solid spheres) having unknown charges 41 and 42. It is found that when they are placed 1 m apart, they experience a 25-N attractive force.

(a) What can you conclude about the charges on these metal marbles from the information given?
(b) The ball bearings are made to touch very briefly and then are separated by 1 m again. What can you conclude about the charges now? Explain.
(c) Suppose that when the charges are 1 m apart, after briefly touching, they again feel a force of 25 N Determine the charges 41 and 42.

Answer 1

a) charges of the opposite, b) Δq = q₄₂-q₄₁, force is repulsive

c) q = 5.27 10⁻⁵ C

Step-by-step explanation:

a) In electrostatic studies it is found that charges of the same sign repel and charges of the opposite sign attract.

On the other hand, as the force between the spheres is attractive, the charges on them are of different sign

b) When the balls touch, the charges are quickly distributed between the two spheres, therefore there are two possibilities:

* if the charges were equal and as they are of the opposite sign, they are neutralized, therefore the spheres remain uncharged

The force between them is zero

* if the charges are different, a residual charge remains

Δq = q₄₂-q₄₁

that is distributed between the two spheres and the force between them is repulsive

c) For this case the charges on the two spheres is equal

q₄₁ = q₄₂ = q

the force is repulsive so the charges are of the same sign.

We can apply Coulomb's law

F =
`k (q_1q_2)/(r^2)`

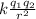
in this case

F =
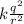
`k (q^2)/(r^2)`

q =
`\sqrt{ (F \ r^2)/(k) }`

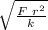
let's calculate

q =
`\sqrt{ (25 \ 1^2)/(9 \ 10^(9)) }` =
`\sqrt{27.7778 \ 10^(-10)}`

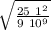q = 5.27 10⁻⁵ C