Question

Which of the following represents z equals negative 5 radical 3 end radical minus 5 times i in trigonometric form?

Answer 1

SOLUTIONS

This is the trigonometric form of a complex number where

`z=-5√(3)-5i`

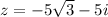
the modulus and

θ

is the angle created on the complex plane.

From the graph, a = r cos θ and b = r sin θ.

z=a+bi

z=rcosθ+irsinθ

z=r(cosθ+isinθ)

`\begin{gathered} r=√(a^2+b^2) \\ r=\sqrt{5√(3))^2+5^2} \\ r=√(75+25) \\ r=√(100) \\ r=10 \end{gathered}`

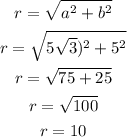
Trigonometric Form of a Complex Number

z=r(cosθ+isinθ)

r is called the modulus and θ is called the argument

Convert between trigonometric form and standard form using

a=rcosθ

b=rsinθ

tanθ=b/a

`\begin{gathered} tan\theta=(b)/(a)=(-5)/(-5√(3))=(1)/(√(3)) \\ \theta=tan^(-1)((1)/(√(3))) \\ \theta=210 \end{gathered}`

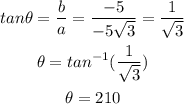
Therefore the trigonometric form will be