Question

3A. Explain in your own words how to find the domain of a function if you know its equation.19-7x6x2+13x-15Be sure to show relevant work.B. Find the domain of f (x) =

Answer 1

From a given function, the domain of the function is the complete possible values of the independent variables. Given a function, the domain of the function could be gotten by finding the solution of the function

For example, a function f(x) as a domain of different values of x

If f(x)= 19-7x, the domain is the solution of the function

`\begin{gathered} f(x)=19-7x \\ 19-7x=0 \\ 19=7x \\ 7x=19 \\ x=(19)/(7) \end{gathered}`

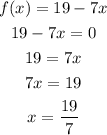
Hence, the domain of a function f(x)= 19-7x is x=19/7

If f(x) of a function is given as

`f(x)=6x^2+13x-15`

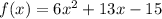
The domain of the function would be the solution of the function

`\begin{gathered} 6x^2+13x-15=0 \\ 6x^2+18x-5x-15_{}=0 \\ 6x(x+3)-5(x+3)=0 \\ (x+3)(6x-5)=0 \end{gathered}`
`\begin{gathered} x+3=0 \\ x=-3 \\ or6x-5=0 \\ 6x=5 \\ x=(5)/(6) \end{gathered}`

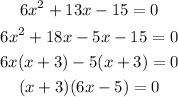
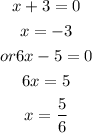
Hence, the domain of the question is x= -3 and x=5/6