ANSWERS
PART A
• Domain: (-∞, ∞)
,
• Graph:
PART B
• x-intercepts: -2, 0, 17
PART C
• Intervals in which g(x) is positive: (-2, 0) U [2, 17)
Step-by-step explanation
PART A
The first part of this function is a cubic function. If factor x² out, we can see clearly what are the roots:
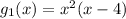
So the roots are x = 0, x = -2 and x = 2.
The second part of the function is a logarithmic function. It starts at x = 2, where the logarithmic part is 0, so its value is 2 at that point and then decreases and intercepts the x-axis at x = 17.
So, the graph of this function is:
As we can see, the graph is continuous for all x, except for x = 2, where it has a jump.
The only restriction is that the argument of the logarithm cannot be zero, but since this happens at x = 1 and that value is where the function is defined as cubic, then there is no restriction there.
Hence, the domain of this function is all real values: (-∞, ∞).
PART B
As explained in part A, the roots of the cubic part of the function are x = -2, x = 0 and x = 2. However, at x = 2 the function is already defined as logarithmic, so the cubic part of the function does not intercept the x-axis at this point.
Additionally, there is another x-intercept given when the second part of the function is 0,
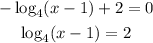
To find x raise 4 to each side of the equation,
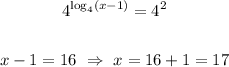
Hence, this function has three x-intercepts: -2, 0, 17.
PART C
Based on the graph, we can describe the intervals for which g(x) is positive:
As we can observe, the function is positive between x = -2 and x = 0, not including these values since the function is 0 there, and also between x = 2 and x = 17, including 2 because the function's value is 2 there, but not 17 because it is a zero.
Hence, the intervals in which the function is positive are (-2, 0) U [2, 17).