The rate of change of a line is equivalent to its slope.
The slope (m) of the line that passes through the points (x₁, y₁) and (x₂, y₂) is calculated as follows:

The line graphed passes through the points (-5, 0) and (0, -5), then its slope is:
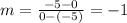
The line of table A passes through the points (6, 11) and (10, 17), then its slope is:
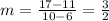
The line of equation B has the slope-intercept form:

with m = -3/2 (the slope) and b = -1.
The line of equation D also has the slope-intercept form with m = 1/2, and b = 3.
The line of table C passes through the points (3, 1) and (7, -3), then its slope is:
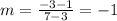
which is the same slope (rate of change) as the function graphed